벡터 그래픽 원리. 겁나 쉽고 정확하게 이해하기
벡터 그래픽 원리에 대해 재밌고 쉽게 이해할 수 있도록 설명하겠습니다. 도대체 왜 벡터 그래픽이라고 부르는 건지 또한 비트맵 그래픽(jpg, png)과는 정확하게 어떤 점이 다른 건지 알아보겠습니다. 끝까지 읽으셨을 때 반드시 얻으시는 것이 있도록 구성했습니다.
시작하기에 앞서 하고 싶은 말은 이 글은 마사지 받는 기분으로 편안하게 봐주셨으면 한다는 것입니다. 원하시는 분이 계실 수도 있어서 수학식도 가볍게 등장하기는 할 것이지만 원하지 않으시면 그 부분은 대충 넘어가셔도 전혀 상관이 없습니다.
벡터 그래픽 원리를 이야기함에 있어서 사실 식은 등장할 필요도 없지만 혹시 모를 니즈를 위해 가볍게 등장할 예정입니다.
먼저 비트맵 그래픽이 무엇인지에 대해 이야기하면 벡터 그래픽 원리는 저절로 이해될 것입니다.
벡터 그래픽과 대조되는 개념 비트맵 그래픽
어떤 사진 파일을 열어서 확대해 본 적이 있으신가요? 확대를 해보시면 그림이 픽셀 단위로 보이며 작은 사각형들이 보이실 겁니다. 그 작은 픽셀들은 그래픽의 최소 단위인데요. 1개의 픽셀은 한 가지 색깔만 가지고 다양한 색깔을 가진 픽셀들이 모여서 복잡한 색감도 나타낼 수 있는 이미지가 표현되는 것입니다.
비트맵이라는 이름은 비트(bit) 단위로 맵(map)을 만드는 방식이라는 뜻입니다.
비트맵 그래픽의 장단점
만약 1,024 x 1,024 픽셀 크기의 이미지가 있다면 100만 개 정도의 작은 조각들이 모여서 그림을 나타낸다는 것인데요. 그만큼 세밀한 색깔 표현이 가능하다는 것이 비트맵의 장점입니다.
하지만 이것은 100만 개씩이나 되는 데이터를 저장해야 한다는 것을 의미합니다. 사진의 크기가 커져서 픽셀의 수가 많아질수록 엄청난 양의 데이터를 저장해야 하고 파일의 용량이 커져야 한다는 것을 의미합니다.
또 다른 치명적인 단점
또 다른 단점은 앞의 단점보다 더 치명적이라기보다는 우리에게 더욱 와 닿을 만한 단점인데요. 비트맵 그래픽은 확대와 축소를 반복하는 과정에서 그래픽이 왜곡되어 깨질 수 있다는 것입니다.
확대할 때 정확히 가로 2배, 세로 2배로 확대를 하면 1개의 픽셀이 똑같은 색깔의 4개의 픽셀로 되면서 왜곡 없이 확대되겠지만, 배수가 정수가 아니게 확대가 되면 새로 생긴 픽셀을 어떤 색깔로 결정해야 하는 지를 선택해야 하는 상황이 생기고 컴퓨터가 어떤 선택을 하던 원본과는 다르게 됩니다.
그래서 확대와 축소를 반복하면 대개 점점 더 왜곡되게 됩니다.
그래서 탄생한 것이 벡터 그래픽(벡터 이미지)
그래서 탄생했다는 말은 벡터 그래픽이 비트맵 그래픽의 단점을 극복하기 위해 고안되었다는 말인데요. 벡터 그래픽은 확대와 축소를 아무리 반복해도 깨지지 않습니다. 또한 아무리 크게 확대해도 같은 화질을 유지합니다.
어떤 원리로 그런 일이 가능하게 하는 걸까요? 비트맵 그래픽은 이미지를 저장 할 때 각각의 픽셀들이 가지는 모든 컬러 값을 저장하는 반면, 벡터 그래픽은 수학 방정식 형태로 데이터를 저장합니다. 그림의 윤곽선을 방정식으로 저장하고 윤곽선 안의 색깔 데이터 또한 저장하게 됩니다.
좀 더 자세하게 그리고 왜 벡터라는 용어가 쓰였는지
여기서 벡터 그래픽에 왜 벡터라는 말이 들어 갔는지를 이야기 할 때가 왔습니다. 벡터는 크기와 방향을 갖는 물리량입니다. 어떤 직선이 있을 때 그 직선의 출발점과 그 출발점에서 끝점까지의 방향과 길이를 나타내는 벡터가 있으면 우리는 그 직선을 특정할 수 있습니다.
이것이 벡터 그래픽이라고 불리는 이유이고 벡터의 개념이 매우 유용하게 사용되고 있음을 볼 수 있습니다.
(※ 만약 수학 식은 별로 보고 싶지 않다면 스크롤을 쭉 내려서 빨간색으로 표시된 자 여기까지부터 읽으시면 됩니다.)
즉 직선 이미지를 저장할 때는
위와 같은 식만 저장하면 그 데이터로 똑같은 직선 이미지를 불러올 수 있습니다.
a는 직선의 출발점이고 v가 출발점에서 끝점까지의 벡터이며 t는 변수입니다.
그리고 곡선의 경우에는 2차 이상의 방정식으로 나타낼 수 있습니다. 벡터 그래픽의 곡선의 나타내는 데에는 아래의 식으로 나타낼 수 있는 베지에 곡선이라는 것이 사용이 됩니다.
이 베지에 곡선이라는 건 벡터 그래픽이라는 것이 개발되는 데 근간이 되었다고 할 수 있는 멋진 개념인데요. 이 개념의 원리에 대해 쉽게 설명되어 있는 글이 있으니 더 공부하실 분은 참고 하시면 되겠습니다.
https://blog.coderifleman.com/2016/12/30/bezier-curves/
※ 위의 주소는 저와는 상관 없는 블로그임을 밝힙니다.
자 여기까지 그림의 윤곽선을 수학 방정식으로 구현할 수 있다는 점만 '아 그래?그렇구나~'하시면 충분합니다.
이제 윤곽선 안의 색깔이 남았는데요. 비트맵 그래픽은 픽셀 단위로 색깔 데이터를 저장하는데 벡터 그래픽의 색깔 구현 원리는 윤곽선에 둘러싸인 면 단위로 색깔 데이터를 저장하는 원리입니다.
만약 아래 그림과 같이 어떤 직선 2개와 어떤 곡선 1개로 둘러 쌓인 면이 초록색이라면, 직선과 곡선의 방정식들과 초록색에 해당하는 컬러값을 데이터로 저장하면 해당 모양의 초록색이 특정되는 것입니다.
벡터 그래픽의 단점
이처럼 벡터 그래픽은 픽셀 단위로 색깔을 저장하지 않고 정해진 면 단위로 색깔을 저장하므로 비트맵 그래픽처럼 디테일하고 세밀한 색 표현에는 적합하지 않습니다. 애초에 비트맵 그래픽처럼 규칙 없이 데이터를 쌩으로 저장하지 않고 수학식을 이용해서 효율성을 확보하는 방식이니까 말입니다.
벡터 그래픽으로 어느 정도 화려한 색깔을 표현하는 방법이 있는데 그래디언트를 이용하는 것입니다. 그래디언트는 수학식으로 표현할 수 있도록 색깔이 점차적으로 변하도록 하기 때문에 이 변화 자체를 수학식으로 표현이 가능해서 픽셀 단위로 데이터를 저장하지 않더라도 화려한 색깔을 표현할 수 있도록 해줍니다.
 |
| 벡터 그래픽 그래디언트 예시 |
비트맵 그래픽처럼 무작위의 다양한 색감을 표현하지는 못하겠지만, 수학적 원리를 이용해서 단순한 색깔 구현에서 벗어날 수 있습니다.
글을 마무리하며
이 문장을 보고 계시다는 것은 글을 끝까지 읽으셨다는 것인데, 진심으로 감사하다는 말씀을 드리겠습니다. 재밌게 보셨다면 잘 봤다는 댓글 가볍게 남겨주시면 감사하겠습니다.
혹여나 제 부족한 글에 수정할 점이 보인다면, 너그러이 이해해 주시고 댓글로서 알려주시면 감사하겠습니다.
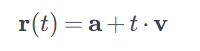
댓글
댓글 쓰기